![]()
![]()
The data set used in this example is available in the example database installed with the software (called "DOE11_examples.rsgz11"). To access this database file, choose File > Help, click Open Examples Folder, then browse for the file in the DOE sub-folder.
The name of the example project is "Reliability DOE - One Factor Reliability DOE."
In this example, one factor reliability DOE is used to determine if there is a difference in three different materials that can be used in a product and, if there is, to determine which material is the best in terms of the product life. 10 units were tested for each material, and the test stopped at 500 hours. The product's life is assumed to follow the Weibull distribution.
The design matrix and the response data are given in the "3 Levels One Factor" folio. The following steps describe how to create this folio on your own.
Choose Insert > Designs > Standard Design to add a standard design folio to the current project.
Click Design Type in the folio's navigation panel, and then select One Factor in the input panel.

Specify that you will be performing reliability DOE by clicking Response 1 in the navigation panel and choosing Life Data from the Response Type drop-down list. Then choose Suspensions from the Censoring drop-down list to specify that some of the data points will be suspensions (i.e., times at which the unit was found not failed).
Define the factor by clicking Factor 1 in the navigation panel and editing its properties in the input panel.
Factor type: Qualitative
Number of levels: 3
Level 1: Type A
Level 2: Type B
Level 3: Type C
Rename the folio by clicking the Experiment1 heading in the navigation panel and entering 3 Levels One Factor for the Name in the input panel.
Click the Additional Settings heading. In the input panel, set the number of Replicates to 10 (since there are ten units tested for each material).
Finally, click the Build icon on the control panel to create a Data tab that allows you to view the test plan and enter response data.
![]()
The data set for this example is given in the "3 Levels One factor" folio of the example project. After you enter the data from the example folio, you can perform the analysis by doing the following:
Note: To minimize the effect of unknown nuisance factors, the run order is randomly generated when you create the design. Therefore, if you followed these steps to create your own folio, the order of runs on the Data tab may be different from that of the folio in the example file. This can lead to different results. To ensure that you get the very same results described next, show the Standard Order column in your folio, then click a cell in that column and choose Sheet > Sheet Actions > Sort > Sort Ascending. This will make the order of runs in your folio the same as that of the example file. Then copy the response data from the example file and paste it into the Data tab of your folio.
In the Distribution drop-down list on the Data tab control panel, select to use the Weibull distribution for the analysis.
Click the Calculate icon on the Data tab control panel.
![]()
The result in the Analysis Summary area show that the p value is 0.032. In other words, there is a 3.2% chance that the variation would be observed in the case when there is no significant difference between the response levels. Since the p value is less than the risk level (10%) entered on the Analysis Settings tab of the control panel, the conclusion is that the different factor levels (i.e., materials) do affect the response.

To see more detailed comparisons of the responses at different factor levels, click the View Analysis Summary icon and view the Life Comparisons table.
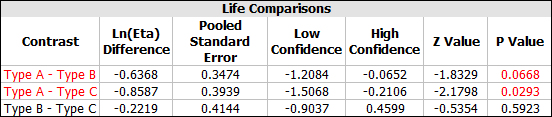
The compared factor levels are listed in the Contrast column (e.g., "Type A - Type B" is the comparison of those two materials). When a p value is red, the compared levels are significantly different. For example, there is a significant difference between the Type A and Type B materials, but there is no significant difference between Type B and Type C.
To see a plot that shows how the product life differs for each material, click the Plot icon.
![]()
Then view the life characteristic plot.
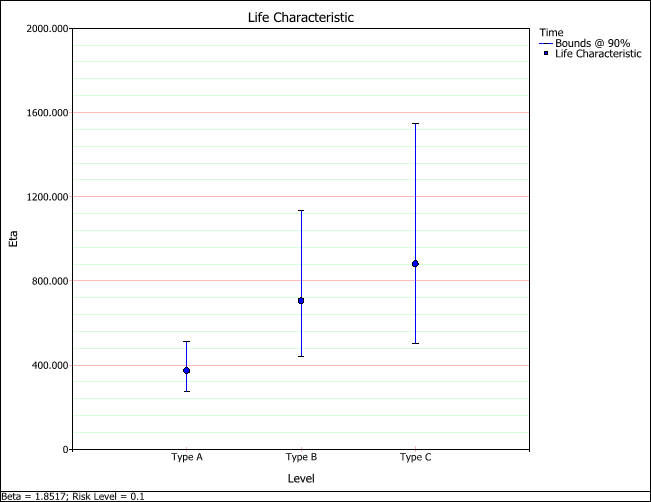
This plot shows the calculated life characteristic for each type of material. The tick marks at the top and bottom of the vertical lines mark the two-sided confidence bounds on the life characteristic. Since the Weibull distribution was used to calculate the data, the life characteristic is eta (i.e., the time at which unreliability = 63.2%).
The analysis showed that the type of material used does affect the product life. From the life characteristic plot, you can see that the Type C material has the largest eta value and therefore the longest expected life.
© 1992-2017. HBM Prenscia Inc. ALL RIGHTS RESERVED.
 |
E-mail Link |