![]()
![]()
The data set used in this example is available in the example database installed with the software (called "DOE11_examples.rsgz11"). To access this database file, choose File > Help, click Open Examples Folder, then browse for the file in the DOE sub-folder.
The name of the example project is "One Factor - Operators in Pulp Mill."
Consider the following experiment, which was performed at a pulp mill. Plant performance is based on pulp brightness, as measured by a reflectance meter. Each of the four shift operators (denoted by A, B, C and D) made five pulp handsheets from unbleached pulp. Reflectance was read for each of the handsheets using a brightness tester. The data set is shown next.
Operator A |
Operator B |
Operator C |
Operator D |
59.88 |
59.87 |
60.83 |
61.01 |
60.12 |
60.32 |
60.87 |
60.87 |
60.88 |
60.42 |
60.56 |
60.69 |
60.98 |
59.99 |
61 |
60.53 |
59.9 |
60.12 |
60.5 |
60.63 |
A goal of the experiment is to determine whether there are significant differences between the operators in making the handsheets and reading their brightness. If there are such differences, then the operators may not be creating the handsheets or recording their observations in a consistent manner.
To determine whether there are differences between the operators, the experimenters create a one-way ANOVA folio. Then they enter the response values for analysis. The design matrix and the response data are given in the "Operator Study - One-Way ANOVA" folio. The following steps describe how to create this folio on your own.
Add a new folio to the current project by choosing Insert > Comparison > One-Way ANOVA.
Right-click the Level 1 column heading and choose Rename Column on the shortcut menu. Change the column name to "Operator A" and click OK.
Rename the second, third and fourth column to "Operator B," "Operator C" and "Operator D," respectively.
The data set for this example is given in the "Operator Study - One-Way ANOVA" folio of the example project. After you enter the data from the example folio, you can perform the analysis by doing the following:
Click the Calculate icon on the Data tab control panel.
![]()
The result in the Analysis Summary area show that the p value is 0.0210. In other words, there is a 2.1% chance that the variation would be observed in the case when there is no significant difference between the response levels. Since the p value is less than the risk level (10%) entered on the Analysis Settings tab of the control panel, the conclusion is that the different factor levels (i.e., operators) do affect the response.

To see more detailed comparisons of the responses at different factor levels, click the View Analysis Summary icon and view the Mean Comparisons table.
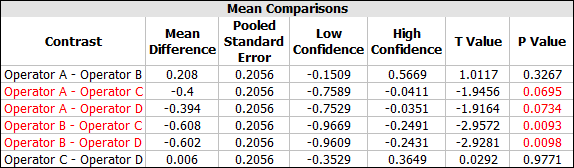
The compared factor levels are listed in the Contrast column (e.g., "Operator A - Operator B" is the comparison of those two operators). When a p value is red, the compared levels are significantly different. For example, there is a significant difference between Operator A and Operator C, but there is no significant difference between Operator A and Operator B.
To see a plot that also allows you to compare the different factor levels, click the Plot icon.
![]()
Then view the box plot. In this plot, you can see that see that operators C and D are nearly the same.
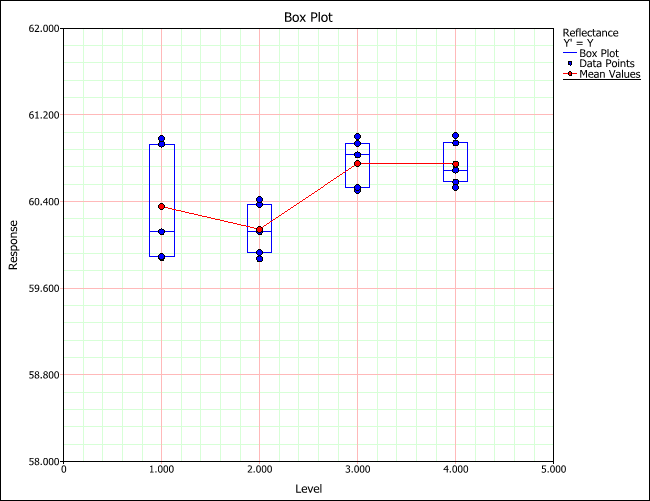
The results show that there is a significant difference between operators A and C, between A and D, and so forth. As a result, the operators receive further training to insure that they create the handsheets and record their observations consistently.
© 1992-2017. HBM Prenscia Inc. ALL RIGHTS RESERVED.
 |
E-mail Link |