

The data set used in this example is available in the example database installed with the software (called "doe9_examples.rsr9"). To access this database file, choose File > Help, click Open Examples Folder, then browse for the file in the DOE sub-folder.
The name of the example project is "Design Evaluation - Taguchi OA vs. Two Level Full Factorial."
Experimenters often need to decide between different experiment designs. For example, a half fractional factorial design with 2 replicates will allow you to estimate the error variance more accurately than a full factorial design which uses the same number of runs, but at the cost of aliasing some effects. A full factorial design will not alias any effects, but it may be more time- and resource-intensive since it requires more factor level combinations.
In this example, the Design Evaluation tool in DOE++ will be used to compare a Taguchi OA design to a two level full factorial design. The designs will be compared in terms of alias structure, detection power and resource constraints. Assume a group of engineers want to investigate the main effects and 2-way interaction effects of 4 factors run at 2 levels each. One option is to use the first 4 columns of the Taguchi L8 (2^7) with 2 replicates; the other option is to use a full factorial design. Both designs require 16 test samples. In the steps that follow, both designs will be evaluated, and the better design will be improved before the engineers agree to use it.
The Taguchi OA design is given in the "Taguchi L8 (2^7)" folio. The four factors were assigned to the first 4 columns under the Additional Settings header on the Design tab.

On the Evaluation Settings page of the control panel, specify that you will solve for power (i.e., the probability that the design will detect an active effect) and select to include all main effects and 2-way interactions in the evaluation.
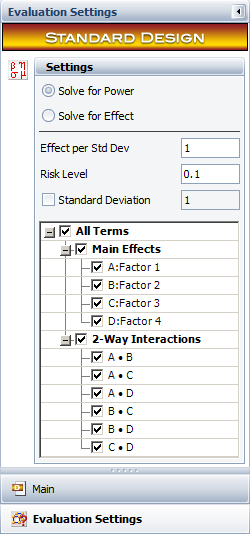
Then click the Calculate icon to return to the Main page of the control panel and view a summary of the evaluation results in the Design Evaluation area.
Click the Detailed Results link in this area to view the calculated power values for each included term, as shown next.
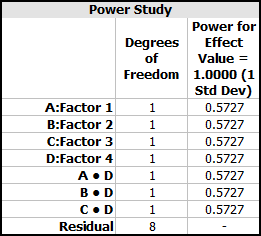
According to this table, if any of the displayed main effects or interaction effects is active, there is a 57.27% chance that the design will detect it.
Notice that some of the interactions that were selected to be included are not shown in the Power Study table. That’s because they are aliased with main effects, as shown in the Alias Structure table.
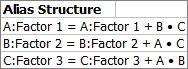
For example, according to this table, the main effect of factor A is aliased with the interaction BC. Thus, BC is not shown in the Power Study table.
The full factorial design is given in the "2^4 Full Factorial Design - 1 Replicate" folio. On the Evaluation Settings page of the control panel, select to solve for power and include all the main effects and 2-way interaction effects.
The calculated power values for the included terms are shown next.
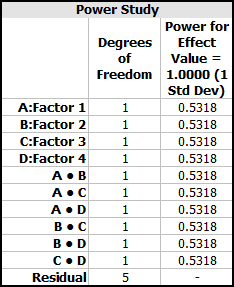
Underneath this table is an indication that "All selected terms are alias free." This means the full factorial design can be used to investigate all the main effects and 2-way interaction effects.
Compare the alias structure
The Taguchi OA design cannot be used to investigate all the 2-way interaction effects. For example, it cannot distinguish the main effect A and the interaction effect BC. The two level full factorial design, however, does not alias any effects. Thus, the full factorial design is better in terms of aliasing.
Compare the detection power
The design evaluation shows that the power for the Taguchi OA design is 0.5727, while the power for the two level full factorial design is 0.5318. The Taguchi OA design might thereby appear better in terms of detection power. However, the two level full factorial design has more terms included in the model (because of its lack of aliasing). If we omit the terms that are aliased in the Taguchi OA design from the full factorial design as well, the power of the full factorial design will also be 0.5727. So in terms of the detection power, both designs are the same.
Consider other factors such as resource constraints
Since there are two replicates in the Taguchi OA design, the error variance can be estimated more accurately. In the two level full factorial design, the error variance is estimated by pooling high order interactions. If some of the interactions are active, the estimated error variance may not be accurate.
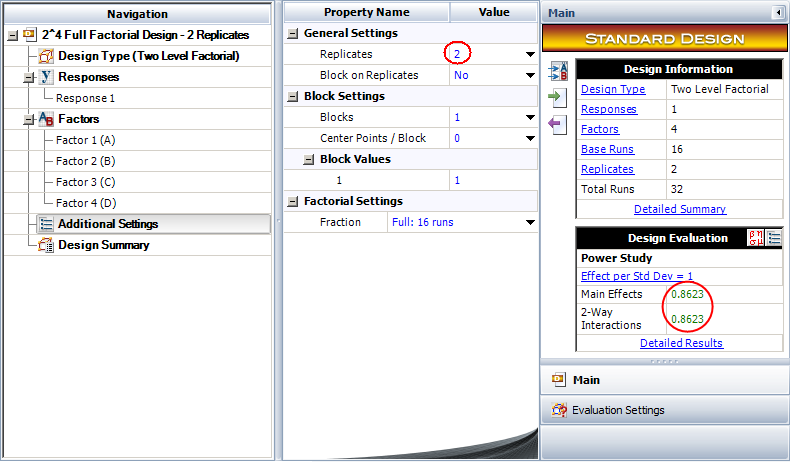
The experimenters decided that the most important goal is to estimate all the main effects and 2-way interactions clearly. Therefore the two level full factorial design is used. Since the power for all the main effects and 2-way interactions is only 0.5318, however, they need to increase the sample size to increase the probability of detecting active effects. So they increase the replicates and recalculate the power values. The effect of the number of replicates on the number of runs and power value is shown in the table below.
| Number of Replicates | Number of Runs | Power |
| 1 | 16 | 0.5318 |
| 2 | 32 | 0.8623 |
| 3 | 48 | 0.9604 |
The experimenters decided to accept any power value above 85%, so they use 2 replicates for this experiment, as shown in the "2^4 Full Factorial Design - 2 Replicates" folio.
© 1992-2015. ReliaSoft Corporation. ALL RIGHTS RESERVED.